Instructor

Prof. Brian Hill

Brief Course Description

We will write programs to solve some of the most interesting problems in mechanics: free fall in a uniform gravitational field, free fall in Newton's Universal Theory of Gravitation, circular planetary motion, elliptical planetary motion, and the fuel burns needed for spacecraft launches. You will need no calculus. Python and Jupyter will do the calculations and graphing. However, you will need the same preparation (Math 12 or Level 3 Math Placement) that you would need if you were about to learn calculus. You will be scratching the surface of the field of computational physics that is used for problems as diverse as quantifying sea-level rise and modeling stellar formation.

Detailed Course Description

Only the very simplest of physics problems can be described with algebra and geometry alone. That said, introductory physics is mostly taught in year-long courses using only algebra, the first semester of such a course focuses mostly on mechanics, and there is already more than enough content in a semester of algebra-based mechanics to prove daunting for most college students.

Furthermore, while daunting, such courses, even when mastered, are simultaneously deeply dissatisfying, because the unifying principles of physics required to tackle harder physics problems require the infinitesimal calculus. Calculus-based physics is mastered by an even fewer number of college students, and yet is one of the greatest and most technologically significant legacies of the human mind. Is there an alternative way to access it?

The answer, I and others believe is "yes," (or this syllabus would not be written), and the means is the field of computational physics, which is typically not taught until at least the fourth semester in an undergraduate's career, despite its fundamental simplicity and its centrality in 21st century physics.

In this course we will approach mechanics using computational physics instead of calculus. As noted in the brief course description above, we will tackle many of the same problems that are tackled in an introductory mechanics course: free fall in a uniform gravitational field, free fall in Newton's Universal Theory of Gravitation, circular orbital motion, elliptical orbital motion, and finally we will compute the transfer orbits that are used to do things like insert satellites into geosynchronous orbit.

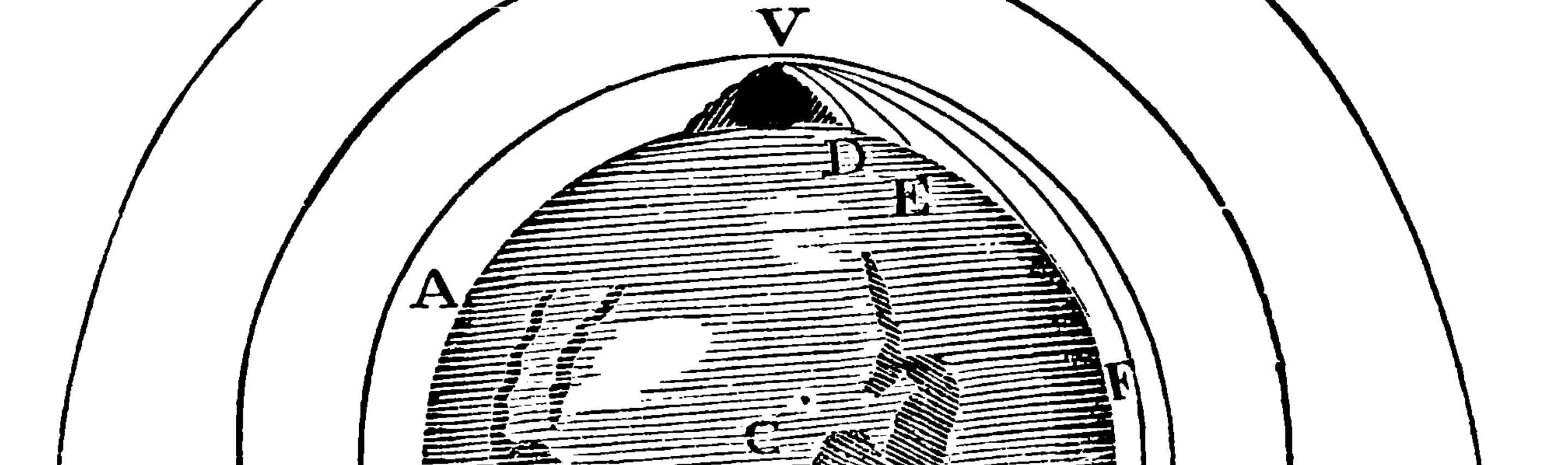
Caption: Newton's thought experiment in Newton's Principia (source: Wikimedia)

We will be able to visualize the solutions to these problems in the same software as we do the Python coding by relying on Jupyter, a full-featured and mature scientific computing environment, which in turn relies on several mature scientific computing and visualization libraries: numpy, matplotlib, and pandas. You will be developing an intuition for calculus, not using the infinitesimal calculus, but by coding in Python to have the computer solve the problems using small temporal steps, and by studying the results of the calculations as they are presented graphically in Jupyter.

To motivate what we will be doing on the computer science front, first imagine that all sorts of people that were creative cooks ran all the restaurants, but that most of them actively avoided aquiring expertise in personnel management and food safety, and furthermore, that there were no city and county health departments that licensed restaurants.

That's the past, present, and future state of the software industry, except cooking is programming, personnel management is project management, and food safety is quality assurance and security. This sounds very bad, but the Wild West state of affairs is on balance a good thing for continued rapid innovation in software. The day software (or physics) becomes a licensed profession is the day it becomes moribund.

To lessen the chance that you will be the cause of the software equivalent of food poisoning, I will try to teach somewhat more than just programming. Specifically, I will have time to include some software development best practices, including documentation, coding style for readability and maintainability, unit testing, working with professional software development tools such as the debugger, and even do a bit of agile project management during the final project phase of the course.

Schedule

Week 1

• Physics & Math: The Description of Motions of Objects in 1-D including Coordinates, Units, Speed, Velocity, and Acceleration.
• Computer Science: Jupyter Notebooks. Documentation in Markdown. Elements of Python including Expressions, Statements, Variables and Assignments, Types (Lists, Tuples, and Ranges), Control Flow (While and For loops), and introducing Functions.

Week 2

• Physics and Math: The Description of Motions of Objects in 2-D. Projectile Motion. Two-Dimensional Acceleration. Newton's Universal Theory of Gravitation
• Computer Science: Continue Discussion of Functions, Scope and Lifetime of Variables. Libraries. Testing. Debugging. Dot Notation for Library Functions and Object Methods.

Week 3

• Physics, Math, and Applications: Circular and Elliptical Orbits. Modeling Battery Charging. Modeling Economic Growth. Kepler's Laws. Energy Conservation.
• Computer Science: Numpy. Mutability, Assignment, and Performance of Python Lists and Numpy Arrays. Second Order Runge-Kutta and Midpoint Method Improvememts to Euler and Euler-Cromer Update Methods. Data Visualization with Pandas.

Week 4

• Final Project: Planning, Selection, Work, and Presentations.

Daily Schedule

• A Daily Schedule is being retrospectively maintained on GitHub.

Final Projects

To give you a chance to build Jupyter notebooks of your own, and to see what a huge variety of fields the methods we are learning can be applied to, the last week (25%) of the class will be devoted to creating and presenting final projects:

• Final Project plan
• Final Project teams

Prerequisites

It would be pointless and circular if a course that is supposed to help you develop an understanding of mechanics and calculus required calculus as a prerequisite. However, the same math that makes one ready for calculus makes one ready for computational physics, and therefore pre-calculus (Math 12 or Level 3 Math Placement) is a prerequisite.

Grading

15% for each of 4 assignments. 15% for midterm (on 2nd Friday, Jan. 17). 25% for final project with presentation to class.

References

Computational Physics

• Numerical Methods for Physics, Alejandro L. Garcia, Pearson, 1994, can be purchased used on AbeBooks. This course draws from Chapters 2 and 3.

Computer Science

• A pedantic Python reference that is ideal for people who have never done any programming is Learn Python 3 The Hard Way (LP3THW). By the way, Python 2 is rapidly becoming obsolete. You should not consider learning it at this point. If you like LP3THW you'll want to buy the PDF. Enough of it is on the web in HTML to get a start and evaluate whether it is right for you.
• We need an environment where we can put the physics, math, and software together without spending an inordinate amount of time building up the basics. Our environment is the Anaconda distribution of Python and Jupyter. Try Jupyter Notebook for Beginners: A Tutorial by Benjamin Pryke.
• Jupyter can be run on-line without installing any software using Binder. That will get us started extra quickly. By using Binder, we can postpone learning how to run Python and Jupyter locally until the 2nd week.
• If you want to put Anaconda on your own machine, you can. The 2019.10 version installed on our lab machines was obtained from the Anaconda Distribution web page. It includes Python 3.7 and Jupyter 6.0.
• Software is complex and easily editable. If you start doing significant projects, the complexity and speed of change make change management essential. The most popular change management system is git. It is a great leap forward from the systems that preceded it (CVS and Subversion). If you want to understand git instead of just memorizing the most common commands, read Travis Swicegood's Pragmatic Guide to Git. After you have used git for a couple of months, take a deep dive into Git Objects to get much clearer on how git works.

Python Labs

All twelve Jupyter Notebooks for the course are in the Loops and Orbits Repository on GitHub. GitHub is cloud hosting for git. You can view the notebooks online. Or you can make a free GitHub account and fork and clone the entire repository. Or you can follow the procedure on page 2 of my directions for using the lab iMacs to download the notebooks one at a time.